Hallo Leute!
Um die Funktionen besser zu erklären sehen wir uns zuerst einmal die wunderschöne Gaußsche Glocke an:
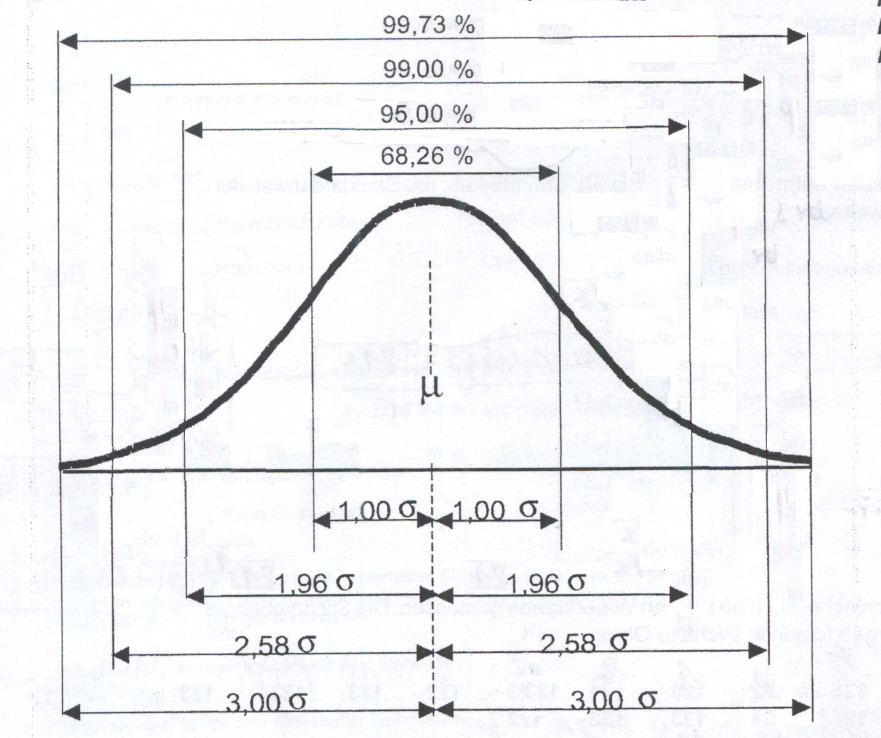
Um Stichproben beurteilen zu können, werden sogenannte Warngrenzen und Eingriffsgrenzen festgelegt. Damit der Prozessverlauf dokumentiert und besser beurteilt werden kann, werden sogenannte Shewhart-Karten eingesetzt. Dabei wird oft die Kombination Mittelwert(xquer) und
Standardabweichung(sigma verwendet. Zum berechnen der Warngrenzen und Eingriffsgrenze
werden die genannten Funktionen eingesetzt:
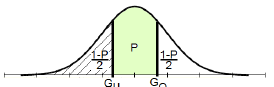
Zu G(u) und Q(u):
Q(u) sind die Anteile , welche sich oberhalb der Grenze Go befinden.
G(u) sind die Anteile, die sich unterhalb der Grenze Gu befinden.
G(u) -Q(u) sind die Anteile welche sich innerhalb von Gu und Go befinden.
Das ist wichtig, um zum Beispiel Anteile berechnen zu können, wenn Gu und Go nicht symmetrisch
von µ sind.
Beispiel:
Bei einem Prozess sind der Mittelwert µ = 21 sigma = 0.28 Go mit 21.7 und Gu mit 20.11 bekannt.
Errechnen Sie wie viel Prozent der Einheiten sich außerhalb von Go und Gu befinden:
0.89 = 21 - 20.11
3.1785714.... = 0.89 / 0.28
G(u) = 0.000740
0.7 = 21.7 - 21
2.5 = 0.7 / 0.28
Q(u) = 0.006210
Q(u) + g(u) = 0.006950 = 0.694968 Prozent
Das sind 6950 ppm (genauer 6949.679059).
Von Gu zu Go sind das etwa 5.678714 sigma, also etwa bei einem Symmetrischen Prozess
2.8392857 sigma von µ aus. Um symmetrisch zu µ liegende Grenzen zu erhalten müsste man diese
auf rund Go = 21.795 und Gu = 20.205 ändern.
Bei diesen Grenzen läge man bei 99.7739 Prozent.
Für den deutschsprachigen Raum auf etwa Go = 21.721 und Gu = 20.279.
Innerhalb der Grenzen von Gu und Go befindet sich der Teil der Produktion die quasi innerhalb der
Warngrenzen bzw. Eingriffsgrenzen sind. Im deutschsprachigen Raum werden 95/99 Prozent, im englischsprachigen Raum 95,44/ 99,97 für EG und WG (Rinne Seite 337) verwendet.
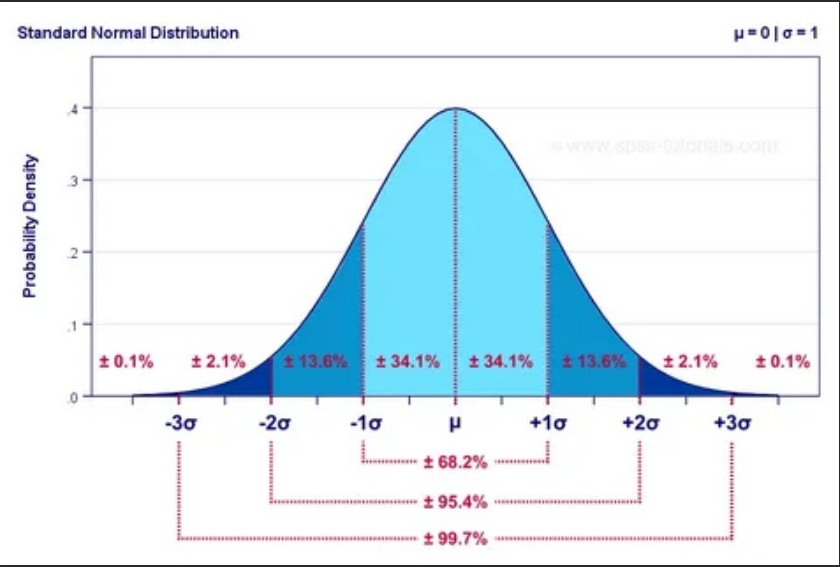
Was das ausmacht?
Bei einer Eingriffsgrenze von 99 Prozent haben wir einen Fehleranteil von aufgerundet 10000 ppm.
ppm heißt das wir auf eine Millionen produzierter Einheiten 10000 fehlerhafte Einheiten haben.
Bei einer Eingriffsgrenze von 99.73 sind das 2700(genauer 2699.796063) fehlerhafte Einheiten.
Aber Vorsicht!
In Europa und im deutschsprachigen Raum werden 7300 Teile mehr als fehlerhaft eingestuft, welche
im englischsprachigen Raum bei diesen Grenzen noch durchgehen würden. Man stelle sich so was
bei der Produktion von Medikamenten vor oder bei wichtigen Maschinenteilen.
Zu den Warngrenzen
Die Warngrenze wird durchaus unterschiedlich gehandhabt. Bei einigen Betrieben sind oft keine zu finden. Wendet man jedoch obere Berechnung dazu auf die Warngrenzen an, so hat man im deutschsprachigen Raum bei einer Warngrenze von etwa 1,96 sigma(95 Prozent)
auf eine Millionen Einheiten etwa 47300, die außerhalb der Warngrenzen liegen, aber innerhalb der Eingriffsgrenzen.
In englischsprachigen Raum bei 95,44 Prozent Warngrenze(etwa 2 sigma Abstand zu µ)
sind das 45500 Teile außerhalb der Warngrenzen und 42800 innerhalb der Eingriffsgrenzen und außerhalb der Warngrenzen.
Wenn Sie zum Beispiel mit dem Auto über eine Brücke fahren, dann korrigieren Sie den Kurs Ihres Fahrzeuges ja auch, bevor Sie ans Brückengeländer krachen oder hinunter stürzen.
Wenn Sie als Lieferant eine Mängelrüge bekommen, weil etwa fehlerhafte Teile in ein Flugzeug eingebaut wurde, ist es für Sie als Lieferant zu spät. Daher gibt es eine kleine Faustregel:
Wenn zwei von drei Stichproben hintereinander außerhalb der Warngrenzen liegen, die letzten Teile der Produktion überprüfen.
Warum Qualitätsprüfung?
Dazu eine kleine Anekdote:
Als ich 2003 in einer kleinen Firma arbeitete, bestellte sich der Chef eine CNC-Fräsmaschine.
Im Gespräch mit dem Händler sagte dieser, das diese Maschinen in Südostasien zusammen gebaut
werden. Diese Firma würde normaler Weise Golfschläger produzieren. Als mein Chef die Nase rümpfte,entgegnete der Händler, diese Firma in Asien kontrolliert ihre Golfschläger unter dem Mikroskop auf Fehler.
So etwas kann sich schon lange keine deutsche Firma mehr leisten. Meiner damaligen Erfahrung nach
beläuft sich der Anteil der Teile, welche im Ausland hergestellt werden und dann quasi als "deutsch"
etikettiert werden auf über 60 Prozent. Einer sagte mir mal, in seiner Firma gäbe es eine extra Abteilung(mit Behinderten, recht so, die brauchen auch Arbeit: vorbildlich) die vornehmlich nichts anderes zu tun haben, als Teile mit dem Aufkleber"Made in Germany" zu behaften.
Ich kenne jemanden, der bei einer Firma arbeitet, welche als Unterlieferant Tauchrohre aus Edelstahl
1.4301 für Stoßdämpfer eines bekannten deutschen Sportwagenherstellers lieferte. Zwar wurden die Teile regelmäßig gemessen, aber diese Messungen nicht dokumentiert. Später bekam der Lieferant Probleme mit seinen Lieferungen. Der Lieferant verlangte von seinen Unterlieferanten die Messprotokolle. Der Chef holte drei seiner Arbeiter ins Büro, erklärte denen den Sachverhalt und ließ
die Arbeiter die Messprotokolle nach Gedächtnis-Protokoll nachschreiben, um es sehr vorsichtig auszudrücken.
1.4301 ist übrigens ein hinterhältiges Material, da es nach und beim Bearbeiten sehr stark zum Verzug neigt.
Verzug von Material kann auch andere Ursachen haben:
Vor Jahren hatten wir den Fall, das eine plangeschliffene Platte ca 400mm x 120mm x 12mm
reklamiert wurde. Bei der Messung war die Ebenheit in Ordnung. Was war passiert? Die Teile wurden im Winter gefertigt und zu uns gebracht. Durch den ständigen Wechsel zwischen warmen und kalten Temperaturen lösten sich die im Material vorhandenen Spannungen und das Werkstück verzog sich sichtbar. Dieser Effekt kann einige Zeit in Anspruch nehmen, so das bei einer Kontrolle, zum Beispiel bei größeren Schweißteilen dieser Effekt erst einige Zeit nach der Prüfung zum Vorschein kommt.
Es hat also nicht unbedingt immer Vorteile schnell zu arbeiten und zu liefern. Viele Firmen haben deswegen einen Teil Ihres Materiallagers im freien. Etwa Firmen für Gussteile.
Zurück zum Stoßdämpfer-Lieferanten.
Anscheinend fiel das mit den Werten auf, man hatte wahrscheinlich die Wirkung des sogenannten cpk-Wertes vergessen.
Der Zusammenhang zwischen cpk-Wert und den sigma-Werten kann man mit einer Faustregel erklären:
je 1 x sigma wäre 1/3 = 0.33333 cpk
2 sigma wäre 2/3 = 0.67 cpk
3 sigma dann 3/3 = 1.0 cpk
4 sigma dann 4/3 = 1.3333333 cpk
5 sigma = 5/3 = 1.67 cpk
6 sigma dann 6/3 = 2.0 cpk
Um diese cpk-Werte von 1,67 oder 1,33 zu erreichen, ist nur möglich, die Messwerte nicht nur innerhalb der Eingriffssgrenzen zu halten, sondern auch in einem bestimmten Abstand davon.
der Prozessfähigkeitsindex cp = Toleranz / (6 * sigma)
gibt den ideal zentrierten Prozess wider.
der cpk = delta_krit / (3 * sigma)
wird mit Hilfe des kleinsten Abstandes der Messwerte zu den Toleranzgrenzen berechnet.
Da reicht eine (er)Findung von Messwerten nicht aus. die Standardabweichung sigma muss innerhalb
bestimmter Werte sein.
Um übrigens Leuten wegen der Bemerkung mit den Behinderten den Wind aus den Segeln zu nehmen:
Mir ist selber eine Firma bekannt, die Ihre knapp über 50 Mitarbeiter zählende Firma in drei Teile
aufgeteilt hatte (drei kleine Firmen). So umgeht man das Gesetz, Behinderte einzustellen, und somit auch eventuelle Umbauarbeiten oder andere Maßnahmen um Kosten zu sparen.
Siehe Sozialgesetzbuch IX(neun) Paragraph 154.
Ich halte nicht viel davon was diese Arbeitgeber tun, da ich mit 30 Prozent selber behindert bin. Das ich etwas gegen Behinderte hätte, diese Bemerkung verbitte ich mir auf das schärfste!
Zurück zum Thema
Wenn man vom Mittelwert µ aus jeweils etwa 2,5758293035489 aus rechnet so befinden sich die da
Eingriffsgrenzen. Je etwa 1,95996398454005 die Warngrenzen.
Die Lage der Grenzen bei der s-Karte können wie folgt berechnet werden.

In Excel oder LibreOffice können die Befehle so aus sehen:
Zunächst für die Mittellinie. Die Bezeichnung 'n' steht für den Stichprobenumfang n
=WURZEL(2/(Stichprobengroesse-1))*((EXP(GAMMALN(n/2)))/(EXP(GAMMALN((Stichprobengroesse-1)/2))))
Mit =Exp(GammaLn(x)) bekommt man den Gammawert selbst.
Bei gcc als compiler bitte Vorsicht walten lasen, da es hier zwei Versionen gibt:
die
gamma()
und die
tgamma()
Funktion
Nun zu den jeweiligen Eingriffsgrenzen und Warngrenzen. Diese werden in den Tabellenkalkulationen mit der Funktion CHIINV berechnet und welche zwei Parameter besitzt:
x und Freiheitsgrade(Stichprobenumfang).
Bei x können folgende Werte im deutschen Raum eingesetzt werden:
OEG = 0.005
OWG = 0.025
UWG = 0.975
UEG = 0.995
Hier ein kleines Programm, welches ich seit kurzem zusammengefasst habe.
Vier Funktionen stammen nicht von mir, Netzfund:
Normalverteilung und Norminv, CHI und CHIINV.
Zuerst zu Norminv .h, welche 'NormalDistribution' und 'NormInv'
Hier die dazu gehörige source:
Nun zu CHIVERT und CHIINV:
der header chiidisp.h:
hier die dazugehörige chiidisp.cpp:
Eine Version von chi-square stammt von mir. Anscheinend kochen alle wie ich mit Wasser und suchen die Werte der EXCEL kompitable Funktion CHIINV ebenso rekursiv. Da die CHIIINV vom Netzfund kürzer ist wie meine, diese.
Die Binomialverteilung, Poissonverteilung und die Funktion Konfidenz stammen von mir. Ich hatte eine Weile Tomaten auf den Augen, bis ich mit der Norminv-Funktion diese fertig hatte. Mit Hilfe der Konfidenz und CHIINV können die Warn- und Eingriffsgrenzen bei der Berechnung
von Shewhart-Karten(s-Karte mit Mittelwert) vorgenommen werden.
Die Verwendung von CHIINV zur Berechnung der Warngrenzen Eingriffsgrenzen sieht dann etwa in Excel so aus:
=ABRUNDEN(((CHIINV(0,005;Stichprobengroesse-1))/(n-1))^0,5; Zahl_der_gewuenschten_Nachkommastellen)
Übrigens:
x^0,5 = Quadratwurzel(x)
Abrunden wieder weg:
=((CHIINV(0,005;Stichprobengroesse-1))/(n-1))^0,5
Mit dem Teil der Formel
sigma_xquer = sigma / Wurzel(Stichprobengröße)
wird die sogenannte innere Streuung berechnet, wobei im Idealfall die Stichprobenmittelwerte innerhalb dieser Grenzen liegen.
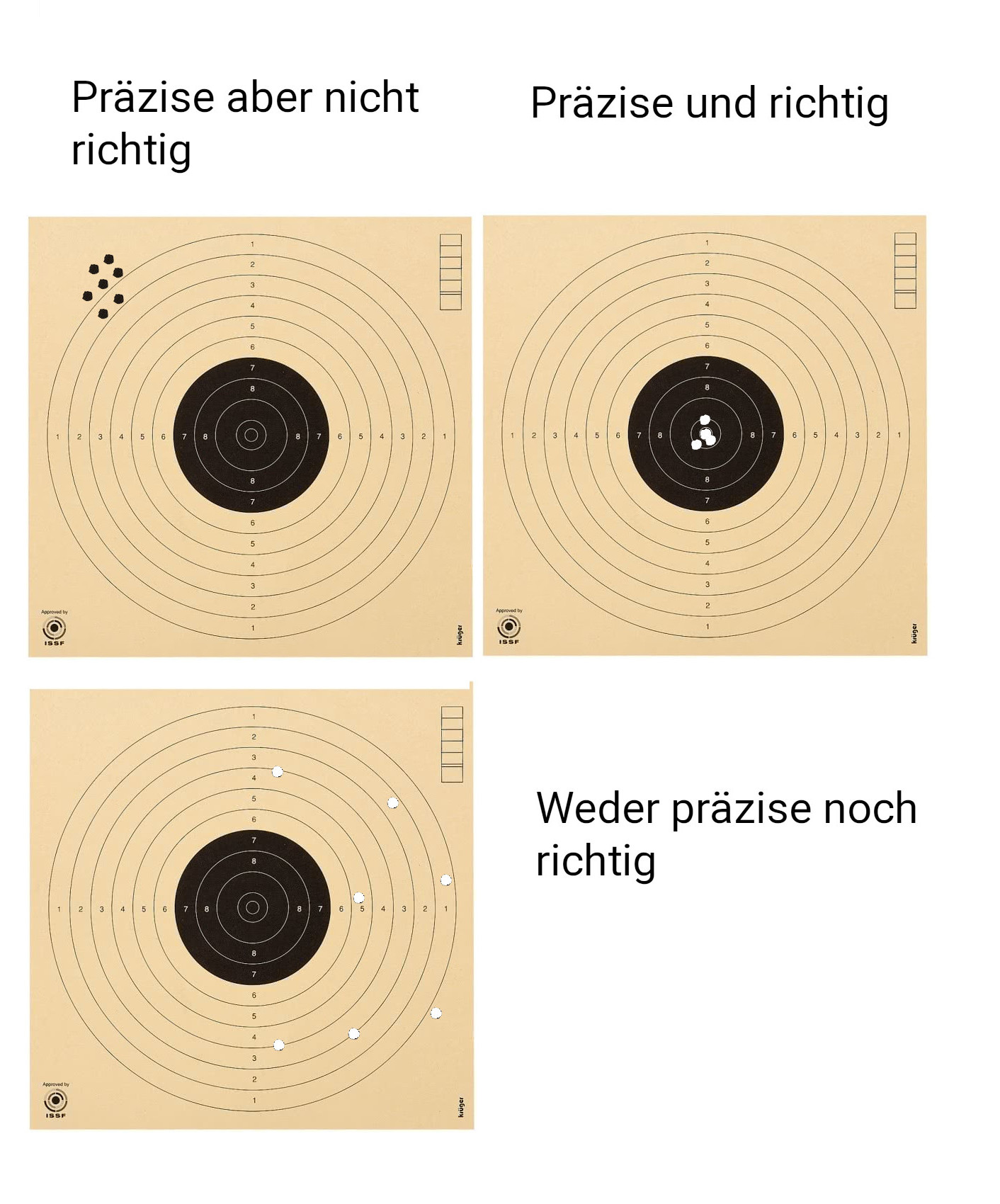
Merke:
genau = präzise und richtig
Nun zur Berechnung der Werte für den Mittelwert. Eine Ausgabe sieht hier etwa so aus:
Berechnung:
n Tabellenkalkulationen kann man mit der Funktion KONFIDENZ arbeiten:
EE = KONFIDENZ(0,01;sigma; Stichprobenumfang)
EW = KONFIDENZ(0,05;sigma; Stichprobenumfang)
Zuerst bestimmt man mit NORINV den sigma-Wart zur Prozentangabe, wie etwa 0.01 oder 0.05.
NORMINV(Zahl;Mittelwert;Standardabweichung);
Der erste Parameter ‚Zahl‘ ist die Größe der Anteile außerhalb der beiden Grenzen Go und Gu in
Prozent / 100. 100 Prozent wäre die Angabe 1.
Für die Berechnung des Abstandes von Go oder Gu zur Mittellinie µ hier folgendes Beispiel:
2,5758293035489 = NORMINV(0,995; 0; 1)
Nun teilt man die Standardabweichung (hier 1 angeben) durch die Wurzel von n und multipliziert das Ergebnis mit dem von Norminv:
EE = Ergebnis_der_Konfidenz=NORMINV(0,995; 0; 1) *(1/WURZEL(10))
Wobei hier 10 bei der Wurzel die Größe der Stichprobe ist.
EW = Ergebnis_der_Konfidenz=NORMINV(0,975; 0; 1) *(1/WURZEL(10))
Man beachte die Änderung der Größe des Parameters bei NORMINV.
Vorher noch einige Mittelwertarten:

Nun einige kleine Funktionen für c und c++. Um den Zugriff zu den Variablen leichter zu gestalten,
verpacken wir die Variablen in eine struct:
Folgende Funktion berechnet einige Arten des Mittelwerts, die Standardabeweichung, den Range, Minimalwert und Maximalwert:
Wer den Medianwert haben will muss die Messwerte der Größe nach ordnen:
Hier noch einige kleine Funktionen:
Nun die Funktionen für CHI-Quadtrat Verteilung:
Das ganze in der Zip zum runterladen mit Beispiel.
Auf
www.libreoffice-forum.de
habe ich meine ganzen Arbeiten zum Thema Qualitätssicherung veröffentlicht. Dann kam mir die Idee, jemand könnte diese Funktionen für c oder cpp gebrauchen. Zum basteln und probieren.
Wer will, kann sich ja mal über diesen Sachverhalt informieren.
Zudem hat c und cpp einen sehr großen Vorteil gegenüber Tabellenkalkulation. Die darin verarbeiteten
Werte können nicht so einfach verändert werden wie in Excel oder Libreoffice. Dazu müßte der Sourcecode umgeschrieben werden. Das geht in einer Firma nicht ohne Wissen von mehreren Leuten.
Mit einer Ausnahme:
Diese Sourcen sollen ausschließlich zur Ausbildung und Weiterbildung dienen. Die kommerzielle Nutzung untersage ich hiermit.
Tut mir leid, aber ich hatte mehrfach schlechte Erfahrungen mit Arbeitgebern. Nix für unguat!
Wenn man schlechte Gedanken hätte könne man meinen, die Qualitätssicherung wird in Zukunft sowieso in der BRD überflüssig sein, da die BRD bald zum globalen Detroit werden könnte. Gerade im Bereich Maschinenbau.
Zu der letzten Annahme eine kleine Anekdote
Ich selbst kenne jemanden sehr gut, der in einer Firma arbeitete, welche nur Teile anderswo prodzuieren ließ, etwa in Tschechien, Bulgarien und verkaufte diese dann als selbst gefertigte. Er mußte zum Beispiel große Schweißteile nach tschechischen Schriftzügen durchsuchen und diese vor der Auslieferung entfernen. Als er Kritik übte, das die Teile nach dem Fehler gefunden wurden und der Projektleiter trotzdem die Teile auslieferte, bekam er folgende Antwort:
"Du musst als Kontrolleur ins Gefängnis, nicht ich, wenn was passiert"
Klar, wenn der Projektleiter durchkommt, war es der böse Kontrolleur der zu viel Wind machte, wenn der Kontrolleur Recht hat, verschwinden einfach ein paar Prüfprotokolle, eh egal schuld hat er sowieso.
Übertrieben? Ich habe da meine eigene Erfahrungen...............
Er war übrigens hocherfreut, als er (endlich) entlassen wurde, da er das nicht mehr mit sich machen lassen wollte.
Qualitätssicherung war ist und bleibt eine der teuersten Abteilungen in einer Firma. Das weglassen von Qualitätssicherung ist übrigens langfristig noch teurer.
Genug der kleinen Bemerkungen.
Schaut einfach mal rein!
Übrigens No Warranty!
Keine Gewähr!
Um die Funktionen besser zu erklären sehen wir uns zuerst einmal die wunderschöne Gaußsche Glocke an:
Um Stichproben beurteilen zu können, werden sogenannte Warngrenzen und Eingriffsgrenzen festgelegt. Damit der Prozessverlauf dokumentiert und besser beurteilt werden kann, werden sogenannte Shewhart-Karten eingesetzt. Dabei wird oft die Kombination Mittelwert(xquer) und
Standardabweichung(sigma verwendet. Zum berechnen der Warngrenzen und Eingriffsgrenze
werden die genannten Funktionen eingesetzt:
Zu G(u) und Q(u):
Q(u) sind die Anteile , welche sich oberhalb der Grenze Go befinden.
G(u) sind die Anteile, die sich unterhalb der Grenze Gu befinden.
G(u) -Q(u) sind die Anteile welche sich innerhalb von Gu und Go befinden.
Das ist wichtig, um zum Beispiel Anteile berechnen zu können, wenn Gu und Go nicht symmetrisch
von µ sind.
Beispiel:
Bei einem Prozess sind der Mittelwert µ = 21 sigma = 0.28 Go mit 21.7 und Gu mit 20.11 bekannt.
Errechnen Sie wie viel Prozent der Einheiten sich außerhalb von Go und Gu befinden:
0.89 = 21 - 20.11
3.1785714.... = 0.89 / 0.28
G(u) = 0.000740
0.7 = 21.7 - 21
2.5 = 0.7 / 0.28
Q(u) = 0.006210
Q(u) + g(u) = 0.006950 = 0.694968 Prozent
Das sind 6950 ppm (genauer 6949.679059).
Von Gu zu Go sind das etwa 5.678714 sigma, also etwa bei einem Symmetrischen Prozess
2.8392857 sigma von µ aus. Um symmetrisch zu µ liegende Grenzen zu erhalten müsste man diese
auf rund Go = 21.795 und Gu = 20.205 ändern.
Bei diesen Grenzen läge man bei 99.7739 Prozent.
Für den deutschsprachigen Raum auf etwa Go = 21.721 und Gu = 20.279.
Innerhalb der Grenzen von Gu und Go befindet sich der Teil der Produktion die quasi innerhalb der
Warngrenzen bzw. Eingriffsgrenzen sind. Im deutschsprachigen Raum werden 95/99 Prozent, im englischsprachigen Raum 95,44/ 99,97 für EG und WG (Rinne Seite 337) verwendet.
Was das ausmacht?
Bei einer Eingriffsgrenze von 99 Prozent haben wir einen Fehleranteil von aufgerundet 10000 ppm.
ppm heißt das wir auf eine Millionen produzierter Einheiten 10000 fehlerhafte Einheiten haben.
Bei einer Eingriffsgrenze von 99.73 sind das 2700(genauer 2699.796063) fehlerhafte Einheiten.
Aber Vorsicht!
In Europa und im deutschsprachigen Raum werden 7300 Teile mehr als fehlerhaft eingestuft, welche
im englischsprachigen Raum bei diesen Grenzen noch durchgehen würden. Man stelle sich so was
bei der Produktion von Medikamenten vor oder bei wichtigen Maschinenteilen.
Zu den Warngrenzen
Die Warngrenze wird durchaus unterschiedlich gehandhabt. Bei einigen Betrieben sind oft keine zu finden. Wendet man jedoch obere Berechnung dazu auf die Warngrenzen an, so hat man im deutschsprachigen Raum bei einer Warngrenze von etwa 1,96 sigma(95 Prozent)
auf eine Millionen Einheiten etwa 47300, die außerhalb der Warngrenzen liegen, aber innerhalb der Eingriffsgrenzen.
In englischsprachigen Raum bei 95,44 Prozent Warngrenze(etwa 2 sigma Abstand zu µ)
sind das 45500 Teile außerhalb der Warngrenzen und 42800 innerhalb der Eingriffsgrenzen und außerhalb der Warngrenzen.
Wenn Sie zum Beispiel mit dem Auto über eine Brücke fahren, dann korrigieren Sie den Kurs Ihres Fahrzeuges ja auch, bevor Sie ans Brückengeländer krachen oder hinunter stürzen.
Wenn Sie als Lieferant eine Mängelrüge bekommen, weil etwa fehlerhafte Teile in ein Flugzeug eingebaut wurde, ist es für Sie als Lieferant zu spät. Daher gibt es eine kleine Faustregel:
Wenn zwei von drei Stichproben hintereinander außerhalb der Warngrenzen liegen, die letzten Teile der Produktion überprüfen.
Warum Qualitätsprüfung?
Dazu eine kleine Anekdote:
Als ich 2003 in einer kleinen Firma arbeitete, bestellte sich der Chef eine CNC-Fräsmaschine.
Im Gespräch mit dem Händler sagte dieser, das diese Maschinen in Südostasien zusammen gebaut
werden. Diese Firma würde normaler Weise Golfschläger produzieren. Als mein Chef die Nase rümpfte,entgegnete der Händler, diese Firma in Asien kontrolliert ihre Golfschläger unter dem Mikroskop auf Fehler.
So etwas kann sich schon lange keine deutsche Firma mehr leisten. Meiner damaligen Erfahrung nach
beläuft sich der Anteil der Teile, welche im Ausland hergestellt werden und dann quasi als "deutsch"
etikettiert werden auf über 60 Prozent. Einer sagte mir mal, in seiner Firma gäbe es eine extra Abteilung(mit Behinderten, recht so, die brauchen auch Arbeit: vorbildlich) die vornehmlich nichts anderes zu tun haben, als Teile mit dem Aufkleber"Made in Germany" zu behaften.
Ich kenne jemanden, der bei einer Firma arbeitet, welche als Unterlieferant Tauchrohre aus Edelstahl
1.4301 für Stoßdämpfer eines bekannten deutschen Sportwagenherstellers lieferte. Zwar wurden die Teile regelmäßig gemessen, aber diese Messungen nicht dokumentiert. Später bekam der Lieferant Probleme mit seinen Lieferungen. Der Lieferant verlangte von seinen Unterlieferanten die Messprotokolle. Der Chef holte drei seiner Arbeiter ins Büro, erklärte denen den Sachverhalt und ließ
die Arbeiter die Messprotokolle nach Gedächtnis-Protokoll nachschreiben, um es sehr vorsichtig auszudrücken.
1.4301 ist übrigens ein hinterhältiges Material, da es nach und beim Bearbeiten sehr stark zum Verzug neigt.
Verzug von Material kann auch andere Ursachen haben:
Vor Jahren hatten wir den Fall, das eine plangeschliffene Platte ca 400mm x 120mm x 12mm
reklamiert wurde. Bei der Messung war die Ebenheit in Ordnung. Was war passiert? Die Teile wurden im Winter gefertigt und zu uns gebracht. Durch den ständigen Wechsel zwischen warmen und kalten Temperaturen lösten sich die im Material vorhandenen Spannungen und das Werkstück verzog sich sichtbar. Dieser Effekt kann einige Zeit in Anspruch nehmen, so das bei einer Kontrolle, zum Beispiel bei größeren Schweißteilen dieser Effekt erst einige Zeit nach der Prüfung zum Vorschein kommt.
Es hat also nicht unbedingt immer Vorteile schnell zu arbeiten und zu liefern. Viele Firmen haben deswegen einen Teil Ihres Materiallagers im freien. Etwa Firmen für Gussteile.
Zurück zum Stoßdämpfer-Lieferanten.
Anscheinend fiel das mit den Werten auf, man hatte wahrscheinlich die Wirkung des sogenannten cpk-Wertes vergessen.
Der Zusammenhang zwischen cpk-Wert und den sigma-Werten kann man mit einer Faustregel erklären:
je 1 x sigma wäre 1/3 = 0.33333 cpk
2 sigma wäre 2/3 = 0.67 cpk
3 sigma dann 3/3 = 1.0 cpk
4 sigma dann 4/3 = 1.3333333 cpk
5 sigma = 5/3 = 1.67 cpk
6 sigma dann 6/3 = 2.0 cpk
Um diese cpk-Werte von 1,67 oder 1,33 zu erreichen, ist nur möglich, die Messwerte nicht nur innerhalb der Eingriffssgrenzen zu halten, sondern auch in einem bestimmten Abstand davon.
der Prozessfähigkeitsindex cp = Toleranz / (6 * sigma)
gibt den ideal zentrierten Prozess wider.
der cpk = delta_krit / (3 * sigma)
wird mit Hilfe des kleinsten Abstandes der Messwerte zu den Toleranzgrenzen berechnet.
Da reicht eine (er)Findung von Messwerten nicht aus. die Standardabweichung sigma muss innerhalb
bestimmter Werte sein.
Um übrigens Leuten wegen der Bemerkung mit den Behinderten den Wind aus den Segeln zu nehmen:
Mir ist selber eine Firma bekannt, die Ihre knapp über 50 Mitarbeiter zählende Firma in drei Teile
aufgeteilt hatte (drei kleine Firmen). So umgeht man das Gesetz, Behinderte einzustellen, und somit auch eventuelle Umbauarbeiten oder andere Maßnahmen um Kosten zu sparen.
Siehe Sozialgesetzbuch IX(neun) Paragraph 154.
Ich halte nicht viel davon was diese Arbeitgeber tun, da ich mit 30 Prozent selber behindert bin. Das ich etwas gegen Behinderte hätte, diese Bemerkung verbitte ich mir auf das schärfste!
Zurück zum Thema
Wenn man vom Mittelwert µ aus jeweils etwa 2,5758293035489 aus rechnet so befinden sich die da
Eingriffsgrenzen. Je etwa 1,95996398454005 die Warngrenzen.
Die Lage der Grenzen bei der s-Karte können wie folgt berechnet werden.
In Excel oder LibreOffice können die Befehle so aus sehen:
Zunächst für die Mittellinie. Die Bezeichnung 'n' steht für den Stichprobenumfang n
=WURZEL(2/(Stichprobengroesse-1))*((EXP(GAMMALN(n/2)))/(EXP(GAMMALN((Stichprobengroesse-1)/2))))
Mit =Exp(GammaLn(x)) bekommt man den Gammawert selbst.
Bei gcc als compiler bitte Vorsicht walten lasen, da es hier zwei Versionen gibt:
die
gamma()
und die
tgamma()
Funktion
Nun zu den jeweiligen Eingriffsgrenzen und Warngrenzen. Diese werden in den Tabellenkalkulationen mit der Funktion CHIINV berechnet und welche zwei Parameter besitzt:
x und Freiheitsgrade(Stichprobenumfang).
Bei x können folgende Werte im deutschen Raum eingesetzt werden:
OEG = 0.005
OWG = 0.025
UWG = 0.975
UEG = 0.995
Hier ein kleines Programm, welches ich seit kurzem zusammengefasst habe.
Vier Funktionen stammen nicht von mir, Netzfund:
Normalverteilung und Norminv, CHI und CHIINV.
Zuerst zu Norminv .h, welche 'NormalDistribution' und 'NormInv'
C++:
// header normiv.h
#ifndef NORMINV_H_INCLUDED
#define NORMINV_H_INCLUDED 3
#include <math.h>
class NormalDistributionConfidenceCalculator
{
public:
NormalDistributionConfidenceCalculator(void);
~NormalDistributionConfidenceCalculator();
/// <summary>
///
/// </summary>
double InverseNormalDistribution(double probability, double min, double max);
/// <summary>
/// Returns the cumulative density function evaluated at A given value.
/// </summary>
/// <param name="x">A position on the x-axis.</param>
/// <param name="mean"></param>
/// <param name="sigma"></param>
/// <returns>The cumulative density function evaluated at <C>x</C>.</returns>
/// <remarks>The value of the cumulative density function at A point <C>x</C> is
/// probability that the value of A random variable having this normal density is
/// less than or equal to <C>x</C>.
/// </remarks>
double NormalDistribution(double x, double mean, double sigma);
/// <summary>
/// Given a probability, a mean, and a standard deviation, an x value can be calculated.
/// </summary>
/// <returns></returns>
double NormInv(double probability);
/// <summary>
///
/// </summary>
/// <param name="probability"></param>
/// <param name="mean"></param>
/// <param name="sigma"></param>
/// <returns></returns>
double NormInv(double probability, double mean, double sigma);
bool AboutEqual(double x, double y);
double NORM_S_VERT(double z);
double konfidenz(double alpha, double sigma, double n);
};
double Epsilon(void);
#endif // NORMINV_H_INCLUDEDHier die dazu gehörige source:
C++:
// source norminv.cpp
#include <iostream>
#include "norminv.h"
NormalDistributionConfidenceCalculator::NormalDistributionConfidenceCalculator(void){};
NormalDistributionConfidenceCalculator::~NormalDistributionConfidenceCalculator(){};
double Epsilon(void)
{
double floatEps = 1;
while (1 + floatEps / 2 != 1)
floatEps /= 2;
return floatEps;
}
double NormalDistributionConfidenceCalculator::InverseNormalDistribution(double probability, double minimal, double maximal)
{
double x = 0;
double a = 0;
double b = 1;
double precision = pow(10, -3);
while ((b - a) > precision)
{
x = (a + b) / 2;
if (NormInv(x) > probability)
{
b = x;
}
else
{
a = x;
}
}
if ((maximal > 0) && (minimal > 0))
{
x = x * (maximal - minimal) + minimal;
}
return x;
}
double NormalDistributionConfidenceCalculator::NormalDistribution(double x, double mean, double sigma)
{
// This algorithm is ported from dcdflib:
// Cody, W.D. (1993). "ALGORITHM 715: SPECFUN - A Portabel FORTRAN
// Package of Special Function Routines and Test Drivers"
// acm Transactions on Mathematical Software. 19, 22-32.
int i;
double del, xden, xnum, xsq;
double result, ccum;
double arg = (x - mean) / sigma;
const double sixten = 1.60e0;
const double sqrpi = 3.9894228040143267794e-1;
const double thrsh = 0.66291e0;
const double root32 = 5.656854248e0;
const double zero = 0.0e0;
//const double min = double.Epsilon;
const double minimal = Epsilon();
double z = arg;
double y = abs(z);
const double half = 0.5e0;
const double one = 1.0e0;
double a[5] =
{
2.2352520354606839287e00, 1.6102823106855587881e02, 1.0676894854603709582e03,
1.8154981253343561249e04, 6.5682337918207449113e-2
};
double b[4] =
{
4.7202581904688241870e01, 9.7609855173777669322e02, 1.0260932208618978205e04,
4.5507789335026729956e04
};
double c[9] =
{
3.9894151208813466764e-1, 8.8831497943883759412e00, 9.3506656132177855979e01,
5.9727027639480026226e02, 2.4945375852903726711e03, 6.8481904505362823326e03,
1.1602651437647350124e04, 9.8427148383839780218e03, 1.0765576773720192317e-8
};
double d[8] =
{
2.2266688044328115691e01, 2.3538790178262499861e02, 1.5193775994075548050e03,
6.4855582982667607550e03, 1.8615571640885098091e04, 3.4900952721145977266e04,
3.8912003286093271411e04, 1.9685429676859990727e04
};
double p[6] =
{
2.1589853405795699e-1, 1.274011611602473639e-1, 2.2235277870649807e-2,
1.421619193227893466e-3, 2.9112874951168792e-5, 2.307344176494017303e-2
};
double q[5] =
{
1.28426009614491121e00, 4.68238212480865118e-1, 6.59881378689285515e-2,
3.78239633202758244e-3, 7.29751555083966205e-5
};
if (y <= thrsh)
{
//
// Evaluate anorm for |X| <= 0.66291
//
xsq = zero;
///if (y > double.Epsilon) xsq = z * z;
if (y > Epsilon() ) xsq = z * z;
xnum = a[4] * xsq;
xden = xsq;
for (i = 0; i < 3; i++)
{
xnum = (xnum + a[i]) * xsq;
xden = (xden + b[i]) * xsq;
}
result = z * (xnum + a[3]) / (xden + b[3]);
double temp = result;
result = half + temp;
}
//
// Evaluate anorm for 0.66291 <= |X| <= sqrt(32)
//
else if (y <= root32)
{
xnum = c[8] * y;
xden = y;
for (i = 0; i < 7; i++)
{
xnum = (xnum + c[i]) * y;
xden = (xden + d[i]) * y;
}
result = (xnum + c[7]) / (xden + d[7]);
xsq = floor(y * sixten) / sixten;
del = (y - xsq) * (y + xsq);
result = exp(-(xsq * xsq * half)) * exp(-(del * half)) * result;
ccum = one - result;
if (z > zero) result = ccum;
}
//
// Evaluate anorm for |X| > sqrt(32)
//
else
{
xsq = one / (z * z);
xnum = p[5] * xsq;
xden = xsq;
for (i = 0; i < 4; i++)
{
xnum = (xnum + p[i]) * xsq;
xden = (xden + q[i]) * xsq;
}
result = xsq * (xnum + p[4]) / (xden + q[4]);
result = (sqrpi - result) / y;
xsq = floor(z * sixten) / sixten;
del = (z - xsq) * (z + xsq);
result = exp(-(xsq * xsq * half)) * exp(-(del * half)) * result;
ccum = one - result;
if (z > zero) result = ccum;
}
///if (result < min)
/// result = 0.0e0;
if (result < minimal)
result = 0.0e0;
return result;
}
double NormalDistributionConfidenceCalculator::NormInv(double probability)
{
const double a1 = -39.6968302866538;
const double a2 = 220.946098424521;
const double a3 = -275.928510446969;
const double a4 = 138.357751867269;
const double a5 = -30.6647980661472;
const double a6 = 2.50662827745924;
const double b1 = -54.4760987982241;
const double b2 = 161.585836858041;
const double b3 = -155.698979859887;
const double b4 = 66.8013118877197;
const double b5 = -13.2806815528857;
const double c1 = -7.78489400243029E-03;
const double c2 = -0.322396458041136;
const double c3 = -2.40075827716184;
const double c4 = -2.54973253934373;
const double c5 = 4.37466414146497;
const double c6 = 2.93816398269878;
const double d1 = 7.78469570904146E-03;
const double d2 = 0.32246712907004;
const double d3 = 2.445134137143;
const double d4 = 3.75440866190742;
//Define break-points
// using Epsilon is wrong; see link above for reference to 0.02425 value
//const double pLow = double.Epsilon;
const double pLow = 0.02425;
const double pHigh = 1 - pLow;
//Define work variables
double q;
double result = 0;
// if argument out of bounds.
// set it to a value within desired precision.
if (probability <= 0)
probability = pLow;
if (probability >= 1)
probability = pHigh;
if (probability < pLow)
{
//Rational approximation for lower region
q = sqrt(-2 * log(probability));
result = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
}
else if (probability <= pHigh)
{
//Rational approximation for lower region
q = probability - 0.5;
double r = q * q;
result = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q /
(((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1);
}
else if (probability < 1)
{
//Rational approximation for upper region
q = sqrt(-2 * log(1 - probability));
result = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
}
return result;
}
double NormalDistributionConfidenceCalculator::NormInv(double probability, double mean, double sigma)
{
double x = NormInv(probability);
return sigma * x + mean;
}
bool AboutEqual(double x, double y) {
double epsilon = std::max(abs(x), abs(y)) * 1E-15;
return abs(x - y) <= epsilon;
}
//Berechnet den Wert der Spalte g(u)
double NormalDistributionConfidenceCalculator::NORM_S_VERT(double z)
{
double quot = 0, wurzel, e, zqh, erge = 0;
//erge = 0.164082975127721 -> bei falsch und 1.333 als z;
//z = 2.58; //758293064439;
wurzel = sqrt(2 * M_PI);
quot = 1 / wurzel;
e = exp(1);
zqh = 0 - ((z * z) / 2);
erge = quot * pow(e, zqh);
return erge;
}
double NormalDistributionConfidenceCalculator::konfidenz(double alpha, double sigma, double n)
{
double wert, innen, dummy, nomin, konfi = 0;
if(alpha > 1) alpha = 0.05;
wert = alpha / 2;
innen = 1 - wert;
dummy = sigma / sqrt(n);
nomin = NormInv(innen);
//std::cout << "monim= " << std::fixed << nomin << std::endl;
konfi = nomin * dummy;
return konfi;
}Nun zu CHIVERT und CHIINV:
der header chiidisp.h:
C++:
// header chiidisp.h
#ifndef CHIIDISB_INC_
#define CHIIDISB_INC_ 3
#include <iostream>
#include <iomanip>
#include <math.h>
#define OEG 0.005
#define OWG 0.025
#define UWG 0.975
#define UEG 0.995
double factorial(double n);
int gerade(int x);
//double gamma(double n);
double chi_square_distribution(double x, double v); // chi square distribution function (v.1)
double chivert(double x, int n);
double _chi_square_distribution(double x, double v); // chi square distribution function (v.2)
double search_chi_square(double x, double h, double p, double v); // recursio search chi square inverse
double chi_square_inverse(double p, double v);
double suche_chiinv(double x, double h, double p, double v); // Recursive Suche von chi square inverse
double chiinv(double p, double v); // chi square inverse
double Get_sKartenLimit(double limit, int n);
double sKarte_anWert(int n);
#endifhier die dazugehörige chiidisp.cpp:
C:
// Datei chiidisb.h
#include "chiidisb.h"
// specific factorial function
double factorial(double n)
{
if (n == 0) { return 1; }
if (n < 0) { return sqrt(M_PI); }
return n * factorial(n - 1);
}
// wenn x gerade rewer = 0, sonst 1
int gerade(int x)
{
int rewer = 0;
if (x % 2 != 0) rewer = 1;
return rewer;
}
/*
// gamma function
double gamma(double n) {
return factorial(n - 1);
}
*/
// chi square distribution function (v.1)
double chi_square_distribution(double x, double v)
{
double a , b, g, f, s, z, p, q;
int k, w;
a = v / 2;
b = x / 2;
// count the Gamma function
g = tgamma(a);
// count of the probability density
f = pow(x, a - 1) / g / exp(b) / pow(2, a);
// count the sum of series
s = 0, z = 0;
k = 0, w = 0;
g = 1;
do {
k = k + 1;
w = w + 2;
z = s;
g = g * (v + w);
s = s + (pow(x, k) / g);
} while (s != z);
// count of probabilities
p = 2 * x * f * (1 + s) / v;
q = 1 - p;
return q;
}
// Eigene Version von chivert
double chivert(double x, int n)
{
double rewer = 0, x_halbe, n_halbe, x_halbe_hoch_k, gwert, kehrwert, expwert, dummy = 0;
double min_x_halbe, k, erfwert;
x_halbe = x / 2;
n_halbe = ((double)n) / 2;
min_x_halbe = 0 - x_halbe;
expwert = exp(min_x_halbe);
if ((gerade(n)) == 0)
{
for (k = 0; k <= (n_halbe - 1); k++)
{
x_halbe_hoch_k = pow(x_halbe, k);
gwert = tgamma(k + 1);
kehrwert = 1.0L / gwert;
dummy += kehrwert * x_halbe_hoch_k;
}
rewer = (expwert * dummy);
}
else
{
erfwert = erf(sqrt(x_halbe));
dummy = 0;
for (k = 0; k <= (n_halbe - 1); k++)
{
gwert = tgamma(k+1.5);
kehrwert = 1.0L / gwert;
dummy += kehrwert * pow(x_halbe, (k+0.5));
}
rewer = 1.0L - (erfwert - exp(min_x_halbe) * dummy);
}
return rewer;
}
// chi square distribution function (v.2)
double _chi_square_distribution(double x, double v)
{
double a, b, f, g, j, p, q, s, z;
int i, k, w;
a = v / 2;
b = x / 2;
// count the Gamma function...
// for even degree
if (int(v) % 2 == 0)
{
g = 1;
for (i = 1; i < a; i++)
g = g * i;
}
// for odd degree
if (int(v) % 2 != 0) {
g = sqrt(M_PI);
for (j = 0.5; j < a; j++) {
g = g * j;
}
}
// count of the probability density
f = pow(x, a - 1) / g / exp(b) / pow(2, a);
// count the sum of series
s = z = 0;
k = w = 0;
g = 1;
do {
k = k + 1;
w = w + 2;
z = s;
g = g * (v + w);
s = s + (pow(x, k) / g);
} while (s != z);
// count of probabilities
p = 2 * x * f * (1 + s) / v;
q = 1 - p;
return q;
}
// recursive suchevon chi square inverse
double search_chi_square(double x, double h, double p, double v)
{
double z = x;
x = x + h;
double y = chi_square_distribution(x, v);
if (z == x || y == p) {
return x;
}
if (y < p) {
return search_chi_square(x - h, h / 2, p, v);
}
if (y > p) {
return search_chi_square(x, h, p, v);
}
return 0; // warning control reaches end of non-void function -wreturn-type
}
// chi shuare inverse
double chi_square_inverse(double p, double v)
{
return search_chi_square(0, 0.1, p, v);
}
// Recursive Suche von chi square inverse
double suche_chiinv(double x, double h, double p, double v)
{
double z = x;
x = x + h;
double y = chivert(x, v);
if (z == x || y == p) return x;
if (y < p) return suche_chiinv(x - h, h / 2, p, v);
if (y > p) return suche_chiinv(x, h, p, v);
return 0; // warning control reaches end of non-void function -wreturn-type
}
// chi square inverse
double chiinv(double p, double v)
{
return suche_chiinv(0, 0.1, p, v);
}
// fuer Shewhart-Karte die Berechnung der Warn und Eingriffsgrenzen siehe DGQ
double Get_sKartenLimit(double limit, int n)
{
double rewer, b, chiwert, quotient;
b = n - 1;
chiwert = chiinv(limit, b);
quotient = chiwert / b;
rewer = sqrt(quotient);
return rewer;
}
// wird zur Berechnung der Werte fuer den Mittelwert der s-Karte benoetigt
double sKarte_anWert(int n)
{
double w, n_halbe, n_min_eins, lnwertb, glna, glnb, rewer;
n_min_eins = (double)n-1;
w = sqrt(2/(n_min_eins));
n_halbe = (double)(n) / 2;
lnwertb = n_min_eins / 2;
glna = lgamma(n_halbe);
glnb = lgamma(lnwertb);
//glnb = log(tgamma(lnwertb));
//std::cout << "glna=" << glna << " glnb=" << glnb << std::endl;
rewer = w * (exp(glna) / exp(glnb));
//rewer = log(tgamma(n));
return rewer;
}Eine Version von chi-square stammt von mir. Anscheinend kochen alle wie ich mit Wasser und suchen die Werte der EXCEL kompitable Funktion CHIINV ebenso rekursiv. Da die CHIIINV vom Netzfund kürzer ist wie meine, diese.
Die Binomialverteilung, Poissonverteilung und die Funktion Konfidenz stammen von mir. Ich hatte eine Weile Tomaten auf den Augen, bis ich mit der Norminv-Funktion diese fertig hatte. Mit Hilfe der Konfidenz und CHIINV können die Warn- und Eingriffsgrenzen bei der Berechnung
von Shewhart-Karten(s-Karte mit Mittelwert) vorgenommen werden.
Die Verwendung von CHIINV zur Berechnung der Warngrenzen Eingriffsgrenzen sieht dann etwa in Excel so aus:
=ABRUNDEN(((CHIINV(0,005;Stichprobengroesse-1))/(n-1))^0,5; Zahl_der_gewuenschten_Nachkommastellen)
Übrigens:
x^0,5 = Quadratwurzel(x)
Abrunden wieder weg:
=((CHIINV(0,005;Stichprobengroesse-1))/(n-1))^0,5
Mit dem Teil der Formel
sigma_xquer = sigma / Wurzel(Stichprobengröße)
wird die sogenannte innere Streuung berechnet, wobei im Idealfall die Stichprobenmittelwerte innerhalb dieser Grenzen liegen.
Merke:
genau = präzise und richtig
Nun zur Berechnung der Werte für den Mittelwert. Eine Ausgabe sieht hier etwa so aus:
Stichproben- größe n | EE | EW |
4 | 1,2879146517744 | 0,9799819922700 |
5 | 1,1519458842342 | 0,8765225405765 |
6 | 1,0515779097005 | 0,8001519460592 |
7 | 0,9735719652775 | 0,7407967545337 |
8 | 0,9106931838592 | 0,6929519121748 |
9 | 0,8586097678496 | 0,6533213281800 |
Berechnung:
Obere Eingriffsgrenze = | μ +AE * σ | 80,008145487463 |
Obere Warngrenze = | μ + AW * σ | 80,006197950323 |
Mittellinie M = | μ | 80 |
Untere Warngrenze = | μ - AW * σ | 79,993802049677 |
Untere Eingriffsgrenze = | μ - AE * σ | 79,991854512537 |
n Tabellenkalkulationen kann man mit der Funktion KONFIDENZ arbeiten:
EE = KONFIDENZ(0,01;sigma; Stichprobenumfang)
EW = KONFIDENZ(0,05;sigma; Stichprobenumfang)
Zuerst bestimmt man mit NORINV den sigma-Wart zur Prozentangabe, wie etwa 0.01 oder 0.05.
NORMINV(Zahl;Mittelwert;Standardabweichung);
Der erste Parameter ‚Zahl‘ ist die Größe der Anteile außerhalb der beiden Grenzen Go und Gu in
Prozent / 100. 100 Prozent wäre die Angabe 1.
Für die Berechnung des Abstandes von Go oder Gu zur Mittellinie µ hier folgendes Beispiel:
2,5758293035489 = NORMINV(0,995; 0; 1)
Nun teilt man die Standardabweichung (hier 1 angeben) durch die Wurzel von n und multipliziert das Ergebnis mit dem von Norminv:
EE = Ergebnis_der_Konfidenz=NORMINV(0,995; 0; 1) *(1/WURZEL(10))
Wobei hier 10 bei der Wurzel die Größe der Stichprobe ist.
EW = Ergebnis_der_Konfidenz=NORMINV(0,975; 0; 1) *(1/WURZEL(10))
Man beachte die Änderung der Größe des Parameters bei NORMINV.
Vorher noch einige Mittelwertarten:
Nun einige kleine Funktionen für c und c++. Um den Zugriff zu den Variablen leichter zu gestalten,
verpacken wir die Variablen in eine struct:
C++:
struct mittelwerte
{
float arimw; // arithmetischer Mittelwert
float geomw; // geometrischer
float harmw; // harmonischer
float quamw; // quadratischer
float stabw; // Standardabweichung sigma
float maxwt; // größter vorkommender Wert einer Stichprobe
float minwt; // kleinster vorkommender Wert einer Stichprobe
float range; // Spannweite
};Folgende Funktion berechnet einige Arten des Mittelwerts, die Standardabeweichung, den Range, Minimalwert und Maximalwert:
C++:
void Mittelwert(float werte[], struct mittelwerte *miwert, int anzahl)
{
int i;
miwert->arimw = 0;
miwert->geomw = 1;
miwert->harmw = 0;
miwert->quamw = 0;
miwert->maxwt = 0;
for (i = 0; i < anzahl; i++)
{
miwert->arimw += werte[i]; // arithmetisch
miwert->geomw *= werte[i]; // geometrisch
miwert->harmw += 1 / werte[i]; // harmonisch
miwert->quamw += (werte[i] * werte[i]);
if (werte[i] > miwert->maxwt) miwert->maxwt = werte[i];
}
miwert->arimw /= anzahl;
miwert->geomw = pow(miwert->geomw, (1 / (double)anzahl));
miwert->harmw = (double)anzahl / miwert->harmw;
miwert->quamw /= (double)anzahl;
miwert->quamw = pow(miwert->quamw, 0.5);
miwert->stabw = 0;
miwert->minwt = miwert->maxwt; // Minimalwert
for (i = 0; i < anzahl; i++)
{
miwert->stabw += (werte[i]-miwert->arimw)*(werte[i]-miwert->arimw);
if (werte[i] < miwert->minwt) miwert->minwt = werte[i];
}
miwert->stabw /= (anzahl - 1); // Standardabweichung
miwert->stabw = pow(miwert->stabw, 0.5);
miwert->range = miwert->maxwt - miwert->minwt;
}Wer den Medianwert haben will muss die Messwerte der Größe nach ordnen:
C:
Diese Funktion berechnet den Medianwert:
// Sortiert ein Array von float-Werten der Größe nach aufsteigend und gibt den Medianwert zurück.
float Sortiere(float (*messwerte)[20], int anzahl)
{
int slei, sleib;
int mw, mwr;
float da, rewer = 0;
for (slei = 0; slei < anzahl; slei++)
for (sleib = slei; sleib < anzahl; sleib++)
{
//cout << endl << " a: " << (*messwerte)[slei] << " b: " << (*messwerte)[sleib];
if ((*messwerte)[slei] > (*messwerte)[sleib])
{
da = (*messwerte)[slei]; //Seite 6
(*messwerte)[slei]= (*messwerte)[sleib];
(*messwerte)[sleib] = da;
}
//cout << endl << " a: " << (*messwerte)[slei] << " b: " << (*messwerte)[sleib] << endl;
}
mw = anzahl / 2;
mwr = anzahl % 2;
if (mwr != 0) rewer = (*messwerte)[mw];
else rewer = ((*messwerte)[mw - 1] + (*messwerte)[mw]) / 2;
//cout << endl << "mwr: " << mwr << " mw= " << mw << " Medianwert: " << rewer;
return rewer;
}Hier noch einige kleine Funktionen:
C:
// specific factorial function
double factorial(double n)
{
if (n == 0) { return 1; }
if (n < 0) { return sqrt(M_PI); }
return n * factorial(n - 1);
}
// wenn x gerade rewer = 0, sonst 1
int gerade(int x)
{
int rewer = 0;
if (x % 2 != 0) rewer = 1;
return rewer;
}Nun die Funktionen für CHI-Quadtrat Verteilung:
C:
// chi square distribution function (v.1)
double chi_square_distribution(double x, double v)
{
double a , b, g, f, s, z, p, q;
int k, w;
a = v / 2;
b = x / 2;
// count the Gamma function
g = tgamma(a);
// count of the probability density
f = pow(x, a - 1) / g / exp(b) / pow(2, a);
// count the sum of series
s = 0, z = 0;
k = 0, w = 0;
g = 1;
do {
k = k + 1;
w = w + 2;
z = s;
g = g * (v + w);
s = s + (pow(x, k) / g);
} while (s != z);
// count of probabilities
p = 2 * x * f * (1 + s) / v;
q = 1 - p;
return q;
}
double chivert(double x, int n)
{
double rewer = 0, x_halbe, n_halbe, x_halbe_hoch_k, gwert, kehrwert, expwert, dummy = 0;
double min_x_halbe, k, erfwert;
x_halbe = x / 2;
n_halbe = ((double)n) / 2;
min_x_halbe = 0 - x_halbe;
expwert = exp(min_x_halbe);
if ((gerade(n)) == 0)
{
for (k = 0; k <= (n_halbe - 1); k++)
{
x_halbe_hoch_k = pow(x_halbe, k);
gwert = tgamma(k + 1);
kehrwert = 1.0L / gwert;
dummy += kehrwert * x_halbe_hoch_k;
}
rewer = (expwert * dummy);
}
else
{
erfwert = erf(sqrt(x_halbe));
dummy = 0;
for (k = 0; k <= (n_halbe - 1); k++)
{
gwert = tgamma(k+1.5);
kehrwert = 1.0L / gwert;
dummy += kehrwert * pow(x_halbe, (k+0.5));
}
rewer = 1.0L - (erfwert - exp(min_x_halbe) * dummy);
}
return rewer;
}
// chi square distribution function (v.2)
double _chi_square_distribution(double x, double v)
{
double a, b, f, g, j, p, q, s, z;
int i, k, w;
a = v / 2;
b = x / 2;
//Seite 9
//Seite 10
// count the Gamma function...
// for even degree
if (int(v) % 2 == 0)
{
g = 1;
for (i = 1; i < a; i++)
g = g * i;
}
// for odd degree
if (int(v) % 2 != 0) {
g = sqrt(M_PI);
for (j = 0.5; j < a; j++) {
g = g * j;
}
}
// count of the probability density
f = pow(x, a - 1) / g / exp(b) / pow(2, a);
// count the sum of series
s = z = 0;
k = w = 0;
g = 1;
do {
k = k + 1;
w = w + 2;
z = s;
g = g * (v + w);
s = s + (pow(x, k) / g);
} while (s != z);
// count of probabilities
p = 2 * x * f * (1 + s) / v;
q = 1 - p;
return q;
}
// recursive suchevon chi square inverse
double search_chi_square(double x, double h, double p, double v)
{
double z = x;
x = x + h;
double y = chi_square_distribution(x, v);
if (z == x || y == p) {
return x;
}
if (y < p) {
return search_chi_square(x - h, h / 2, p, v);
}
if (y > p) {
return search_chi_square(x, h, p, v);
}
return 0; // warning control reaches end of non-void function -wreturn-type
}
// chi shuare inverse
double chi_square_inverse(double p, double v)
{
return search_chi_square(0, 0.1, p, v);
}
// Recursive Suche von chi square inverse
double suche_chiinv(double x, double h, double p, double v)
{
double z = x;
x = x + h;
double y = chivert(x, v);
if (z == x || y == p) return x;
if (y < p) return suche_chiinv(x - h, h / 2, p, v);
if (y > p) return suche_chiinv(x, h, p, v);
return 0; // warning control reaches end of non-void function -wreturn-type
}
// chi square inverse
double chiinv(double p, double v)
{
return suche_chiinv(0, 0.1, p, v);
}
// fuer Shewhart-Karte die Berechnung der Warn und Eingriffsgrenzen siehe DGQ
double Get_sKartenLimit(double limit, int n)
{
double rewer, b, chiwert, quotient;
b = n - 1;
chiwert = chiinv(limit, b);
quotient = chiwert / b;
rewer = sqrt(quotient);
return rewer;
}
// wird zur Berechnung der Werte fuer den Mittelwert der s-Karte benoetigt
double sKarte_anWert(int n)
{
double w, n_halbe, n_min_eins, lnwertb, glna, glnb, rewer;
n_min_eins = (double)n-1;
w = sqrt(2/(n_min_eins));
n_halbe = (double)(n) / 2;
lnwertb = n_min_eins / 2;
glna = lgamma(n_halbe);
glnb = lgamma(lnwertb);
//glnb = log(tgamma(lnwertb));
//std::cout << "glna=" << glna << " glnb=" << glnb << std::endl;
rewer = w * (exp(glna) / exp(glnb));
//rewer = log(tgamma(n));
return rewer;
}Das ganze in der Zip zum runterladen mit Beispiel.
Auf
www.libreoffice-forum.de
habe ich meine ganzen Arbeiten zum Thema Qualitätssicherung veröffentlicht. Dann kam mir die Idee, jemand könnte diese Funktionen für c oder cpp gebrauchen. Zum basteln und probieren.
Wer will, kann sich ja mal über diesen Sachverhalt informieren.
Zudem hat c und cpp einen sehr großen Vorteil gegenüber Tabellenkalkulation. Die darin verarbeiteten
Werte können nicht so einfach verändert werden wie in Excel oder Libreoffice. Dazu müßte der Sourcecode umgeschrieben werden. Das geht in einer Firma nicht ohne Wissen von mehreren Leuten.
Mit einer Ausnahme:
Diese Sourcen sollen ausschließlich zur Ausbildung und Weiterbildung dienen. Die kommerzielle Nutzung untersage ich hiermit.
Tut mir leid, aber ich hatte mehrfach schlechte Erfahrungen mit Arbeitgebern. Nix für unguat!
Wenn man schlechte Gedanken hätte könne man meinen, die Qualitätssicherung wird in Zukunft sowieso in der BRD überflüssig sein, da die BRD bald zum globalen Detroit werden könnte. Gerade im Bereich Maschinenbau.
Zu der letzten Annahme eine kleine Anekdote
Ich selbst kenne jemanden sehr gut, der in einer Firma arbeitete, welche nur Teile anderswo prodzuieren ließ, etwa in Tschechien, Bulgarien und verkaufte diese dann als selbst gefertigte. Er mußte zum Beispiel große Schweißteile nach tschechischen Schriftzügen durchsuchen und diese vor der Auslieferung entfernen. Als er Kritik übte, das die Teile nach dem Fehler gefunden wurden und der Projektleiter trotzdem die Teile auslieferte, bekam er folgende Antwort:
"Du musst als Kontrolleur ins Gefängnis, nicht ich, wenn was passiert"
Klar, wenn der Projektleiter durchkommt, war es der böse Kontrolleur der zu viel Wind machte, wenn der Kontrolleur Recht hat, verschwinden einfach ein paar Prüfprotokolle, eh egal schuld hat er sowieso.
Übertrieben? Ich habe da meine eigene Erfahrungen...............
Er war übrigens hocherfreut, als er (endlich) entlassen wurde, da er das nicht mehr mit sich machen lassen wollte.
Qualitätssicherung war ist und bleibt eine der teuersten Abteilungen in einer Firma. Das weglassen von Qualitätssicherung ist übrigens langfristig noch teurer.
Genug der kleinen Bemerkungen.
Schaut einfach mal rein!
Übrigens No Warranty!
Keine Gewähr!
