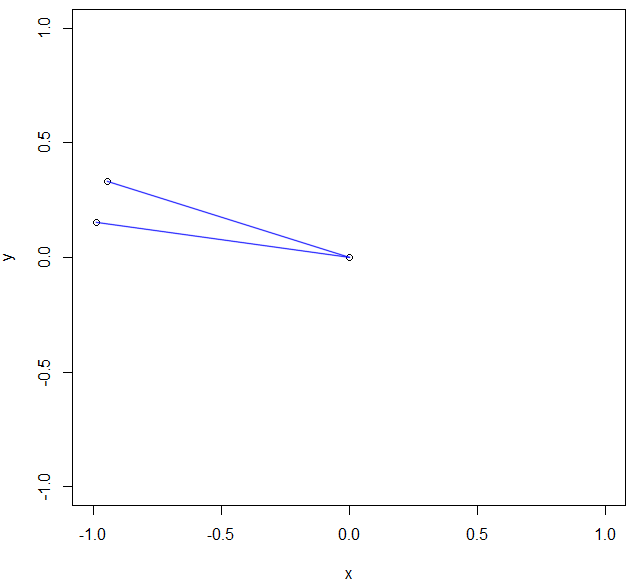
Ich habe gerade ein vermeintlich triviales trigonometrisches Problem. Ich habe zwei Punkte, die zusammen mit dem Ursprung ein "offenes" Dreieck bilden. Eigentlich nicht wirklich ein Dreieck, sondern eher so eine Art "offener Sektor". Die Koordinaten der Punkte sind im Beispiel P1 = (-0,9886; 0,1505) und P2 = (-0,9431; 0,3325). Sieht so aus:
Nun kommt ein weiterer Punkt dazu. Beispiel: P3 = (-0,9664; -0,2569). Sieht so aus:
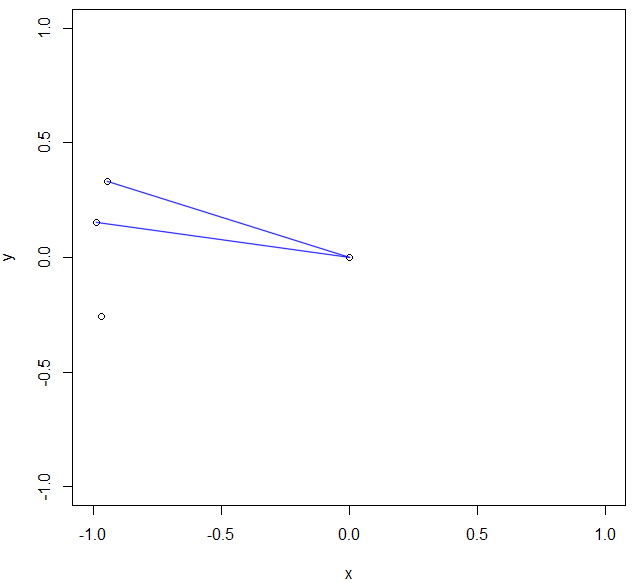
Die Frage lautet: Liegt der neue Punkt im Sektor? Mit Hingucken leicht zu beantworten, die Antwort lautet: "Nein". Wie kann ich das programmatisch lösen? Die "Arme" des Sektors können auch kürzer oder länger sein, das Ganze kann sich in allen vier Quadranten abspielen und auch über Quadrantengrenzen hinweg. Falls das wichtig ist: Die Koordinaten der Punkte sind das Ergebnis aus der Umrechnung von Polarkoordinaten in euklidische Koordinaten, der Sektor ergibt sich eigentlich aus Richtungsangaben (Richtung 1: 278°, Richtung 2: 289°, Richtung des dritten "Punktes": 255°). Hat da jemand ne allgemeingültige Idee? Stehe aufm Schlauch, wüsste nichtmal, wonach ich google-n sollte.
Nun kommt ein weiterer Punkt dazu. Beispiel: P3 = (-0,9664; -0,2569). Sieht so aus:
Die Frage lautet: Liegt der neue Punkt im Sektor? Mit Hingucken leicht zu beantworten, die Antwort lautet: "Nein". Wie kann ich das programmatisch lösen? Die "Arme" des Sektors können auch kürzer oder länger sein, das Ganze kann sich in allen vier Quadranten abspielen und auch über Quadrantengrenzen hinweg. Falls das wichtig ist: Die Koordinaten der Punkte sind das Ergebnis aus der Umrechnung von Polarkoordinaten in euklidische Koordinaten, der Sektor ergibt sich eigentlich aus Richtungsangaben (Richtung 1: 278°, Richtung 2: 289°, Richtung des dritten "Punktes": 255°). Hat da jemand ne allgemeingültige Idee? Stehe aufm Schlauch, wüsste nichtmal, wonach ich google-n sollte.